As Estatísticas de Localização, também conhecidas como Medidas de Tendência Central ou Medidas de Posição, são grandezas que visam a estimar um ponto central na amostra ou um valor intermediário em torno do qual os elementos de uma série estão distribuídos. As grandezas mais conhecidas desse tipo são a Média Aritmética, a Mediana e a Moda.
Em uma distribuição simétrica, a Média, a Mediana e a Moda coincidem (possuem os mesmos valores).
Média Aritmética ( ou μ)
ou μ)
A média aritmética é frequentemente considerada uma das medidas de posição mais importante.
Definição e Cálculo
- Geral: É calculada como a soma de todas as observações de uma variável, dividida pela quantidade total de observações (ou número de elementos, n).
- Simbologia: É representada por
para a média amostral e por μ para a média populacional.
- Outros Nomes: Pode ser conhecida como Esperança ou Valor Esperado.
- Dados Agrupados (Categorizados): No caso de variáveis contínuas em faixas (dados categorizados), utiliza-se a técnica do ponto médio, que consiste em considerar que todas as observações de uma determinada categoria estão concentradas no ponto médio da respectiva classe.
Propriedades
- Sensibilidade a Extremos: A média é sensível à presença de valores atípicos (outliers) ou valores extremos. Por ser atraída pelos valores extremos, ela não é uma estimativa robusta.
- Soma dos Desvios: A soma de todos os desvios em relação à média aritmética é sempre igual a zero.
- Existência e Unicidade: A média aritmética existe e é sempre única para qualquer tipo de amostra.
Mediana
A mediana é uma medida de posição que divide igualmente os valores.
Definição e Cálculo
- É o valor que ocupa a posição central de um conjunto ordenado de dados, dividindo o conjunto em duas partes de igual número de observações (50% para um lado e 50% para o outro).
- Para ser calculada, a lista de valores (o Rol) exige que os dados estejam organizados em ordem crescente ou decrescente.
- Para N ímpar: A mediana é o próprio elemento central, encontrado na posição (n+1)/2.
- Para N par: A mediana corresponde à média aritmética dos dois termos centrais.
- Dados Agrupados (Categorizados): Em distribuições de frequência categorizadas (variáveis contínuas), a mediana é calculada pela interpolação linear, utilizando uma fórmula que leva em conta o limite inferior da classe mediana e as frequências acumuladas e absolutas.
Propriedades
- Robustez: A mediana é uma estimativa robusta. Ela não é sensível à presença de outliers (valores extremos). Devido à sua robustez, é frequentemente utilizada em substituição à média em situações onde há muitos outliers.
Moda
A moda se refere ao valor mais frequente em uma amostra.
Definição e Modalidade
- É o valor que apresenta a maior frequência da variável entre os valores observados. A moda sempre estará no ápice do gráfico de distribuição.
- Distribuição Unimodal: Possui uma única moda.
- Distribuição Bimodal: Possui duas modas.
- Distribuição Amodal: Não possui nenhuma moda (nenhum valor se repete mais que os demais).
- Classe Modal: Em dados agrupados (variáveis contínuas), a classe modal é a categoria que apresenta a maior frequência absoluta.
Propriedades e Cálculo em Dados Agrupados
- Robustez: Assim como a mediana, a moda é uma estimativa robusta, ou seja, não é sensível a valores extremos.
- Cálculo Agrupado: Para dados categorizados, pode ser estimada pela:
- Moda Bruta: Tomando o ponto médio da classe modal.
- Fórmula de Czuber: Uma expressão que considera o limite inferior da classe modal e as frequências da classe anterior e posterior.
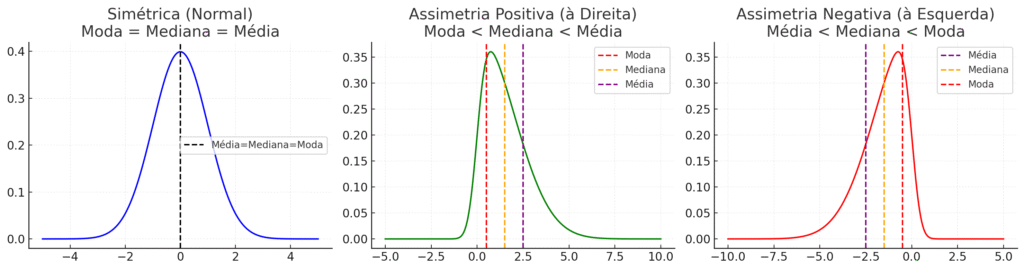
Relação entre Média, Mediana e Moda (Assimetria)
A relação entre essas medidas é utilizada para determinar a assimetria (grau de assimetria) de uma distribuição. A média aritmética é a medida que mais sofre influência dos extremos e, portanto, quem define a assimetria.
| Assimetria | Relação das Medidas | Característica Gráfica |
| Simétrica (Normal) | Moda=Mediana=Média | Curva perfeitamente simétrica em relação à média. |
| Positiva (à Direita) | Moda<Mediana<Média | A cauda mais longa está voltada para a direita. |
| Negativa (à Esquerda) | Média<Mediana<Moda | A cauda mais longa está voltada para a esquerda. |
Além disso, o estatístico Pearson propôs uma relação que pode ser utilizada para estimar a Moda, a diferença entre a média e a moda é igual ao triplo da diferença entre a média e a mediana:
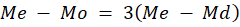
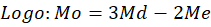
👉 Quer mais resumos como este? Acompanhe nosso blog e prepare-se para o seu concurso!
