Os juros compostos são amplamente considerados a base da matemática financeira e são a lógica seguida pela maior parte das aplicações e financiamentos no mercado. Eles são popularmente conhecidos como a “oitava maravilha do mundo”, segundo uma citação frequentemente atribuída a Einstein.
Conceito e Funcionamento
No regime de juros compostos, a principal característica é que ocorre a capitalização de juros. Isso significa que a cada período de capitalização, todo o saldo da aplicação é capitalizado — tanto o principal quanto os juros anteriormente acumulados. Dessa forma, os juros são calculados sobre o capital inicial acrescido dos rendimentos dos períodos anteriores.
A capitalização de juros faz com que a dívida cresça de forma mais acelerada ao longo do tempo. A progressão do montante acumulado em juros compostos segue uma progressão geométrica.
O montante final (M) acumulado em uma operação de juros compostos é calculado pela expressão:
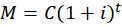
onde C é o capital inicial, i é a taxa de juros e t é o tempo decorrido para que aconteçam as capitalizações. Para calcular os juros (J), a recomendação é sempre calcular o montante final e obter os juros como a diferença entre o montante final e o capital inicial (J = M – C).
Tipos de Taxas de Juros
- Taxa Nominal e Taxa Efetiva: Quando a taxa de juros informada está em um período diferente da capitalização (exemplo: 12% ao ano capitalizada mensalmente), ela é chamada de taxa de juros nominal. As contas financeiras não devem ser feitas usando a taxa nominal. A taxa nominal deve ser convertida em uma taxa efetiva que corresponda ao período da capitalização. É crucial lembrar que, para essa conversão, a Taxa de Juros Nominal é sempre proporcional à Taxa de Juros efetiva, mesmo que a operação seja de juros compostos.
- Taxas Equivalentes: Duas taxas de juros são consideradas equivalentes quando, no regime de juros compostos, elas produzem o mesmo montante final quando aplicadas ao mesmo capital e pelo mesmo tempo. Para encontrar taxas equivalentes, utiliza-se a comparação de potências.
Comparação com Juros Simples
A relação entre juros simples (JS) e juros compostos (JC) depende do tempo da aplicação, medido na mesma unidade da taxa de juros:
- JS = JC: Quando o tempo é igual a 1 período.
- JS > JC: Quando o período de tempo é inferior a 1 (por exemplo, menos de um ano se a taxa for anual).
- JC > JS: Quando o período de tempo é superior a 1. O efeito do tempo no acúmulo de juros compostos é maior que nos juros simples, e essa diferença se torna sensivelmente maior à medida que o tempo passa.
Propriedades e Aplicações
- Cindibilidade do Prazo: O Regime de Juros Compostos possui a propriedade de cindibilidade do prazo. Isso significa que é indiferente se a aplicação é mantida continuamente ou se o prazo é “quebrado” e reaplicado, contanto que o prazo global permaneça o mesmo. Graças a essa propriedade, os juros compostos são o modo natural de se fazer investimentos.
- Taxa Real e Aparente: Para descontar o efeito da inflação sobre um rendimento (taxa aparente), é utilizada a relação:
- Desconto Composto: O desconto composto utiliza o regime de capitalização composta. O desconto racional composto (ou desconto por dentro) é o tipo mais importante, sendo utilizado para decisões de investimento e cálculo do fluxo de caixa descontado. A fórmula do valor atual (Ad) para o desconto racional composto é:
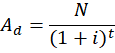
onde N é o valor nominal do título. Para descontos compostos, a taxa efetiva é sempre calculada com base no desconto racional composto.
- Sistemas de Amortização: Os juros em sistemas de amortização como o Francês (Tabela Price) e o SAC (Sistema de Amortização Constante) são capitalizados a cada período de pagamento seguindo a dinâmica dos juros compostos. No sistema francês, por exemplo, o cálculo das prestações uniformes leva em conta a equivalência financeira a juros compostos.
